Complex Number Calculator in Rust

To get started in Rust, I implemented a calendar. It can perform calculations with real numbers as well as with complex numbers. It also provides some functions for calculating sums or products. I then used egui to create a GUI for it.

GUI

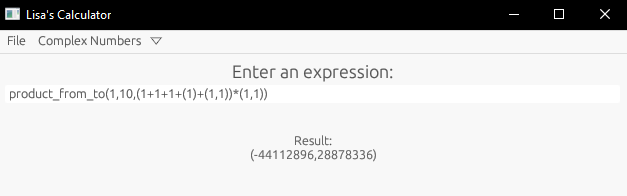
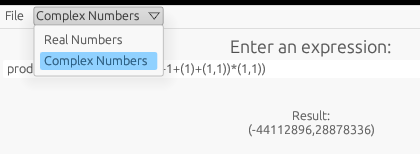
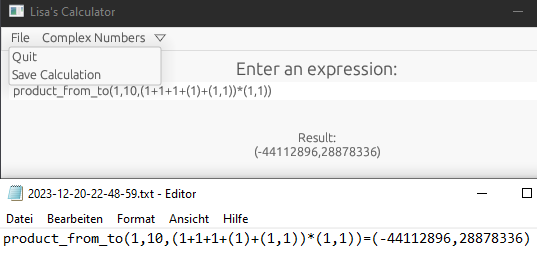
Users can save the arithmetic expression and its result to a file.

Generic Traits for Solids

The source code of my calculator can be extended easily to work with any solid, not just real or complex numbers. Therefore, I moved the code for performing the actual calculations into a Rust Trait solid.

pub trait Solid<T : SolidNumber<T>> : Sized {
        //general info
        fn get_solid_name() -> String;

        //addition
        fn get_neutral_element_addition() -> T;
        fn add(x : T, y : T) -> T;
        fn get_additive_inverse(x : T) -> T;

        //multiplication
        fn get_neutral_element_multiplicative() -> T;
        fn multiply(x : T, y : T) -> T;
        fn get_multiplicative_inverse(x : T) -> T;

        //other functions
        fn get_available_functions() -> Vec<(String, fn(Vec<String>)->(T, String), Vec<i32>, i32)>;
}

This generic traits is used for implementing real and complex numbers:

use std::fmt::Display;
use chrono::format::parse;
use crate::calculations::calculator::calculatorfunctions::{Calculator, has_enclosing_brackets, split_to_expressions};
use crate::calculations::calculator::solid::solid::{get_standard_methods, PrintableNumber, Solid, SolidNumber};
use crate::calculations::solids::realnumbers::RealNumbers;

pub struct ComplexNumbers{

}

pub struct ComplexNumber {
    a : f64,
    b : f64,
}



impl Solid<ComplexNumber> for ComplexNumbers{
    fn get_solid_name() -> String {
        return "Complex Numbers".to_string();
    }

    fn get_neutral_element_addition() -> ComplexNumber {
        return ComplexNumber { a: 0.0, b: 0.0 };
    }

    fn add(x: ComplexNumber, y: ComplexNumber) -> ComplexNumber {
        return ComplexNumber {a : x.a+y.a, b: x.b+y.b};
    }

    fn get_additive_inverse(x: ComplexNumber) -> ComplexNumber {
        return ComplexNumber {a : -x.a, b: -x.b};
    }

    fn get_neutral_element_multiplicative() -> ComplexNumber {
        return ComplexNumber{ a: 1.0, b: 0.0 }
    }

    fn multiply(x: ComplexNumber, y: ComplexNumber) -> ComplexNumber {

        let a = x.a;
        let b = x.b;
        let c = y.a;
        let d = y.b;
        return ComplexNumber{
            a : a * c - b * d,
            b: a * d + c * b
        };
    }

    fn get_multiplicative_inverse(x: ComplexNumber) -> ComplexNumber {
        let nenner = (x.a.powi(2) + x.b.powi(2));
        return ComplexNumber{a: x.a/ nenner,b: -(x.b/nenner)};
    }

    fn get_available_functions() -> Vec<(String, fn(Vec<String>) -> (ComplexNumber, String), Vec<i32>, i32)> {
        return get_standard_methods::<ComplexNumber, ComplexNumbers>();
    }
}


impl PrintableNumber for ComplexNumber {
    fn to_sn_string(&self) -> String {
        return format!("({},{})",self.a,self.b)
    }
}

impl SolidNumber<ComplexNumber> for ComplexNumber {
    fn is_number(s: &str) -> bool {
        if !has_enclosing_brackets(&s.to_string()) {
            if Calculator::<f64, RealNumbers>::parse(s).1==""{
                return true;
            }
            if s.eq("i"){
                return true;
            }

            return false;
        }
        else{
            let numbers = split_to_expressions(&s.to_string(), vec![',']);

            if  numbers.0.len()!=2{
                return false;
            }
            //println!("complex number: a={}, b={}", numbers.0[0], numbers.0[1]);
            let a = Calculator::<f64, RealNumbers>::parse(numbers.0[0].as_str());
            let b = Calculator::<f64, RealNumbers>::parse(numbers.0[1].as_str());

            if (a.1!="") | (b.1!=""){
                return false;
            }

            return true;
        }
    }

    fn from_string(s: String) -> ComplexNumber {
        if s.eq("i"){
            return ComplexNumber{a: 0.0, b: 1.0};
        }
        let parsedFloat = Calculator::<f64, RealNumbers>::parse(s.as_str());
        if parsedFloat.1==""{
            return ComplexNumber{a : parsedFloat.0, b: 0.0};
        }

        let numbers = split_to_expressions(&s.to_string(), vec![',']);
        let a = Calculator::<f64, RealNumbers>::parse(numbers.0[0].as_str());
        let b = Calculator::<f64, RealNumbers>::parse(numbers.0[1].as_str());
        return ComplexNumber {a: a.0, b: b.0 };

    }


}

You can also find this project here:

GitHub

Comments

Feel free to leave your opinion or questions in the comment section below.

By clicking on 'Sign in with Github', a login cookie is created. You can undo this at any time by clicking 'Delete Cookie'.