Die atemberaubenden Abenteuer der Algo-Ameisen
Eine Kurzgeschichte über das Finden von kürzesten Wegen
Die atemberaubenden Abenteuer der Algo-Ameisen und ihrer allwissenden Alliierten - Eine anschauliche Abhandlung
Ein genialer Gedanke
Müde hob die Ameisenkönigin Amanda ihr Haupt, dass sie zuvor auf einem ihrer sechs Beine hatte ruhen lassen. „Sprich, Ameise“, verkündete sie mit einer nasalen Stimme und wandte ihren Blick der kleinen Ameise zu, die sich vor ihrem Thron niedergekniet hatte. Diese begann, zu sprechen: „Verehrte Königin, ich komme mit einer Idee, die unsere Produktivität und die Einnahmen im Handel mit den anderen Ameisenkolonien deutlich erhöhen könnte.“ Die Königin wackelte nun etwas interessierter mit ihren Antennen. „Mein Name ist Iffi, ich bin die Informatik-Ameise in unserem Bau. Neulich ist mir aufgefallen, dass die Wege, die wir benutzen, wenn wir zu den anderen Ameisenhügeln krabbeln, nicht immer die kürzesten sind, die man auf unserer Wiese nehmen könnte. Unser Straßensystem ist zwar bestmöglich ausgebaut und verwendet soweit es die Umgebung zulässt die direkten Routen, die es zwischen den Hügeln gibt, aber es scheitert an unserer Logistik. Oft nehmen unsere Trupps, die Waren zu anderen Kolonien hin oder von diesen hertransportieren, eine lange Strecke, auch wenn es eine Abfolge von Straßen gäbe, die zum gleichen Ziel führt und viel kürzer ist. Um es genau zu sagen, sie laufen einen Umweg.“
„Und wie gedenkst du, dieses Problem zu beheben, Ameise?“, fragte die Ameisenkönigin.
„Unsere Karten müssen erneuert werden. Wir müssen messen, wie lange wir von einem Ameisenhügel zum nächsten brauchen und für alle Ameisenhügel herausfinden, wie man am schnellsten von unserem Ameisenbau zu diesem hin kommt.“
„Das klingt nach einem aufwändigen Unterfangen“, vermutete die Ameisenkönigin.
Iffi nickte zustimmend: „Das ist leider wahr. Ich brauche die Unterstützung von allen Ameisen im Bau, und zwar gleichzeitig. Der normale Arbeitsbetrieb muss für diese Zeit pausiert werden, allerdings dauert das Verfahren nicht lang und am Ende ist unser ganzes Einzugsgebiet kartographiert und ausgeschildert.“
Ameisenkönigin Amanda rümpfte die Nase; Die Vorstellung, dass der Verkehr in ihrem Bau komplett pausiert werden müsste, passte ihr gar nicht. Das bedeutete finanzielle Einbußen und gefährdete ihren Jahresplan. Andererseits erkannte sie, dass die Optimierung der Reiserouten eine sinnvolle Investition der Ameisenarbeitszeit war.
„Dein Vorhaben findet meine Anerkennung und die Umsetzung sei dir gestattet“, verkündete sie also. „Aber ich will, dass unter keinen Umständen Zeit verschwendet wird. Daraus soll kein Wandertag werden. Kein Ameisenhügel soll mehrmals abgelaufen werden. Das ist meine Bedingung.“
„Kein Problem“, sagte Iffi und grinste, kurz vergessend, sich an den etablierten Ameisenadelssprech zu halten. Die Königin hatte zwar eine herablassende und wichtigtuerische Art, aber im Grunde genommen war sie eine vernünftige Ameise. Sie hörte ihren Untergebenen zu und verstand sofort, was man ihr erzählte.
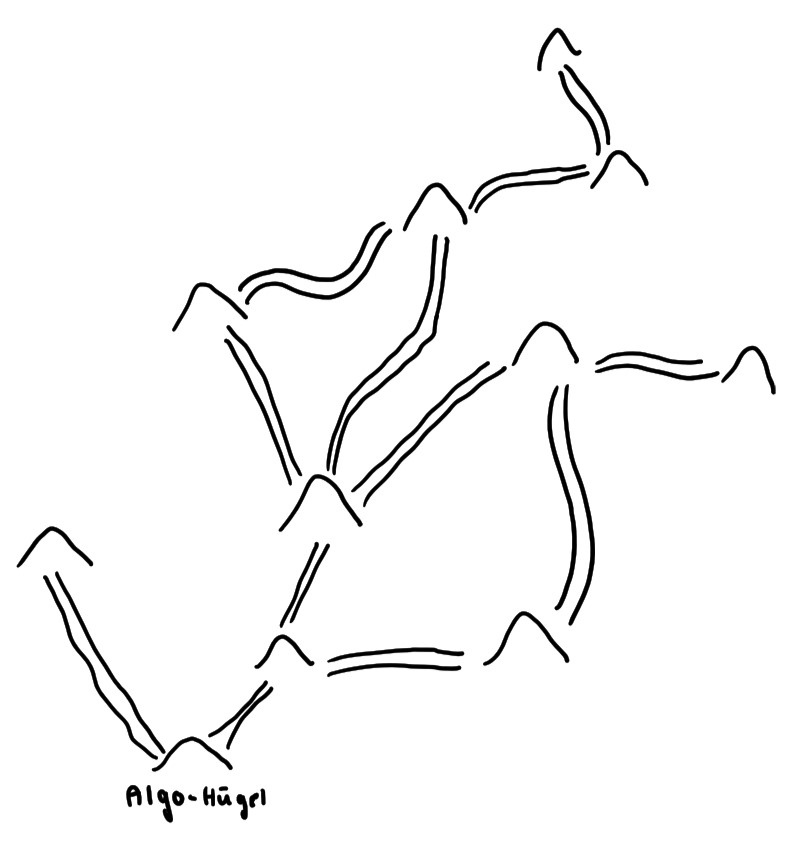Das Netz der AmeisenhügelDirekt am nächsten Tag sollte Iffis Plan in die Tat umgesetzt werden. Kurz vor acht Uhr morgens waren alle Ameisen vor dem Bau versammelt. Iffi erhob die Stimme.
„Alle mal herhören. Wir sind hier gerade eine Menge von n Ameisen. Vor uns befinden sich eine Anzahl von k Wegen, auf denen wir heute noch keine Fußspuren hinterlassen haben. Wir teilen uns jetzt auf. n/k Ameisen nehmen den ersten, n/k Ameisen den zweiten und n/k Ameisen den k-ten Weg. Wenn ihr an einem Ameisenhügel ankommt, wo noch kein Schild steht, haut ihr dort eins in den Boden und schreibt die seit Beginn vergangene Zeit und den Hügel, von dem ihr gerade gekommen seid, drauf. Dann teilt ihr euch auf die Wege, die von dem Hügel ausgehen und noch keine Fußspuren von uns haben, auf, und macht dasselbe nochmal. Und nochmal. Und nochmal. Das macht ihr solange, bis ihr entweder am Ende unseres Gebiets ankommt oder an einen Ameisenhügel gelangt, wo schon ein Schild steht. Im letzteren Fall sind dort schon andere von uns gewesen, die einen kürzeren Weg zu diesem Hügel gelaufen sind. Dann orientiert ihr euch an den gesetzten Schildern und lauft denselben Weg den ihr gekommen seid zum Ameisenbau zurück. Hier tragt ihr dann alle Hügel, bei denen ihr gewesen seid, mitsamt der Zeit in die da drüben aushängende Liste ein. Noch Fragen?“
„Ja“, rief eine Ameise von ganz hinten, „Was machen wir, wenn wir mit einer Gruppe von n Ameisen an einem Hügel stehen, aber n < k gilt? Dann haben wir nicht genug Ameisen, um alle weiteren Wege abzulaufen.“
Iffi antwortete: „Dieser Fall wird nicht eintreten. Du kannst n = ∞ annehmen. Und weißt du auch warum? Wir sind die Algo-Ameisen. Die stolzen Ameisen vom Hügel Algo. Wir sind die größte und tollste Ameisenkolonie auf der ganzen Wiese!“
Die Menge jubelte und die Ameisen streckten zustimmend ihre Vorderbeine in die Höhe. Iffi schüttelte sich innerlich, aber das gehörte nunmal dazu.
Um Punkt acht Uhr ertönte der Startschuss. Alle Ameisen, Iffi miteingeschlossen, krabbelten los. Natürlich alle mit der gleichen Geschwindigkeit, Ameisenmarschtempo 3. Wenn ein Team schneller oder langsamer laufen dürfte als die anderen, würde das das Ergebnis verfälschen. Iffi hoffte, dass die Ameisen kein Wettrennen daraus machen würden und sich auch an alle anderen Absprachen halten würden. Und tatsächlich wurde sie nicht enttäuscht: Nachdem das letzte Team zurückgekehrt war, konnte sie eine wunderschöne neue Karte anfertigen, die die optimalen Transportrouten darstellte.
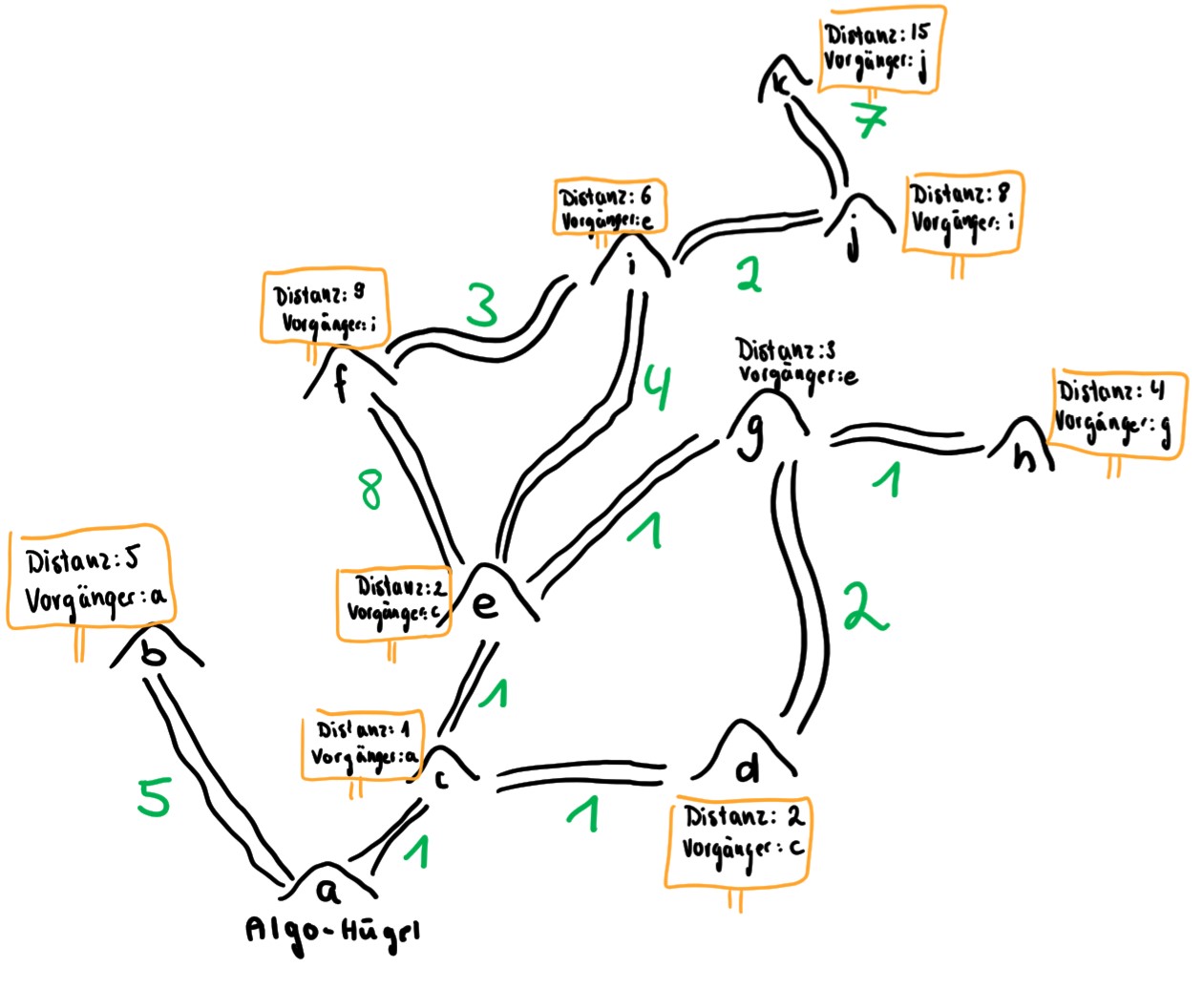Die Beschilderung der Ameisenhügel nach Iffis Plan
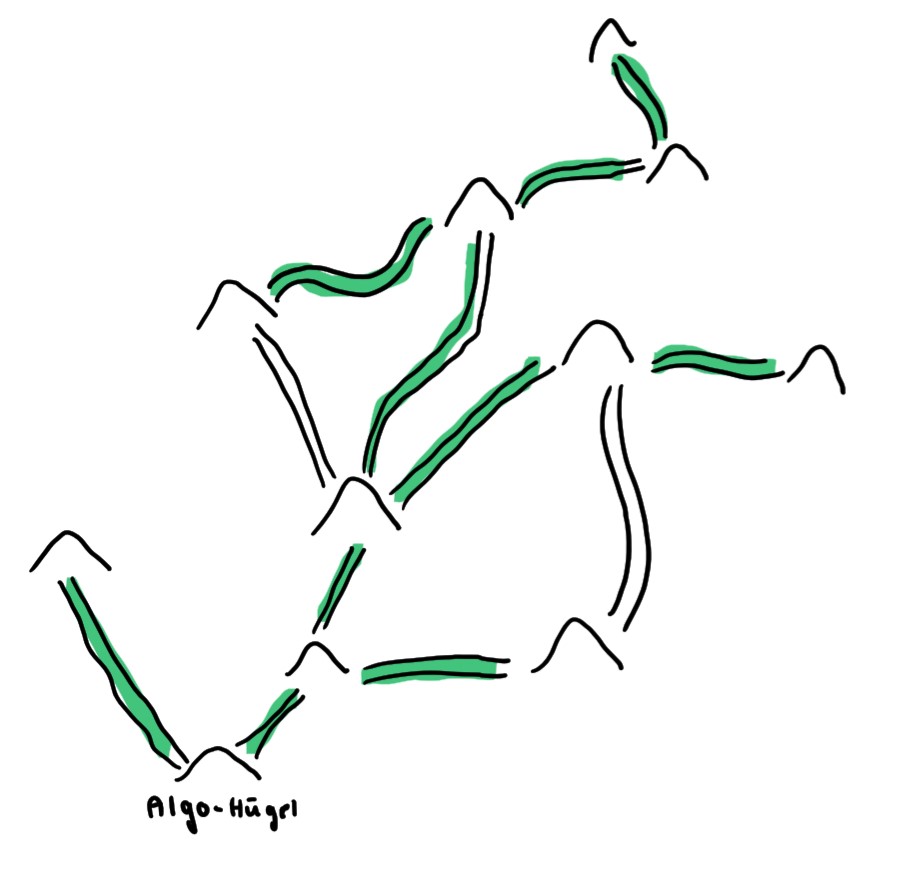Kürzeste Transportrouten vom Algo-Hügel zu den anderen HügelEin gemächliches Gespräch
„Ganz schön pfiffig für eine einzelne Ameise“, meinte Wanda die Weinbergschnecke zur Partnerschnecke Timmi.
„Wohl wahr“, meinte Timmi und schielte ehrlich beeindruckt mit den Stielaugen auf die herumwuselnden Ameisen hinab. „Das Problem, die kürzesten Wege von einem Punkt aus zu finden, ist ein Problem aus der Graphentheorie. Iffis Lösungsidee hat zwar gut funktioniert und ist korrekt, lässt sich allerdings nicht direkt auf Graphen übertragen.“
„Das stimmt“, meinte Wanda und nickte im Schneckentempo. „Ein Graph ist ein Tupel (V,E) mit einer Menge Knoten V und einer Menge Kanten E. Die Knoten sind hier die Ameisenhügel und die Kanten die Ameisenstraßen. Das Kantengewicht entspricht der Zeit, die die Ameisen für eine Straße brauchen. Die Ameisentrupps, die von Hügel zu Hügel laufen und die Schilder verteilen, lassen sich allerdings nicht auf diese Strukturen übertragen. Wenn wir Iffis Idee in Pseudocode notieren wollten, wüsste ich nicht, wie ich die sich gleichzeitig fortbewegenden und sich immer weiter aufteilenden Einheiten umsetzen würde. Es gibt bestimmt eine Möglichkeit, das eleganter zu lösen.“
In der nächsten halben Stunde raspelten Wanda und Timmi stumm auf ihren Löwenzahnblättern vor sich hin, bis Timmi meinte: „Ich hab eine Idee.“
„Lass mal hören“, sagte Wanda.
„Für jeden Hügel x betrachten wir ja jeden von ihm ausgehenden Weg. Wenn die Nachbarhügel, die sich am Ende von den Wegen befinden, noch kein Schild haben und ein Ameisentrupp von Hügel x aus zu ihnen aufbricht, ist es ja sehr wahrscheinlich, dass der Trupp dort ein Schild setzt. Es sei denn, ein anderer Trupp kommt ihnen zuvor, während sie auf dem Weg dahin sind.“
„Ja und?“
„Wir gehen jetzt einfach davon aus, dass unser Ameisentrupp von Ameisenhügel x bei allen direkt verbundenen Ameisenhügeln zuerst ankommt und setzen dort ein Schild, sobald wir den noch nicht besuchten Ameisenhügel entdeckt haben. Und wenn dann doch noch ein anderer Ameisentrupp kommt, der einen schnelleren Weg gefunden hat, kann dieser das Schild ja austauschen. So können wir in unserem Algorithmus von Knoten zu Knoten springen und müssen nicht darüber nachdenken, wo wann welcher Ameisentrupp steckt.“
„Das find ich gut“, meinte Wanda, „aber wie legen wir fest, in welcher Reihenfolge wir uns die Knoten anschauen? Das spielt ja auch eine Rolle.“
Timmi meinte: „Wir schauen uns immer den Knoten als nächsten an, der von den verbliebenen den geringsten Abstand zum Startknoten hat.“
„Hey Moment, das kommt mir bekannt vor“, meinte Wanda, „Das ist doch der Dijkstra-Algorithmus! Dazu kenne ich den Pseudocode!“
Eine erschreckende Erkenntnis
Iffis Unterfangen zum Finden der kürzesten Wege zwischen den Ameisenhügeln war ein voller Erfolg gewesen. Mithilfe der neuen Karte konnten die Warentransporte schneller und der Handel effektiver durchgeführt werden. Einige Zeit später erfuhr Iffi, dass sich das Ameisen-Wegesystem verändert hatte. Ein paar abenteuerlustige Ameisen hatten einige neue Wege zwischen den Ameisenhügeln entdeckt, die ebenfalls als Handelsrouten geeignet waren. Daher holte Iffi sich die Erlaubnis der Ameisenkönigin Amanda ein, ihr Verfahren erneut ausführen zu dürfen, um zu überprüfen, ob durch die neuen Wege schnellere Routen verwendet werden können.
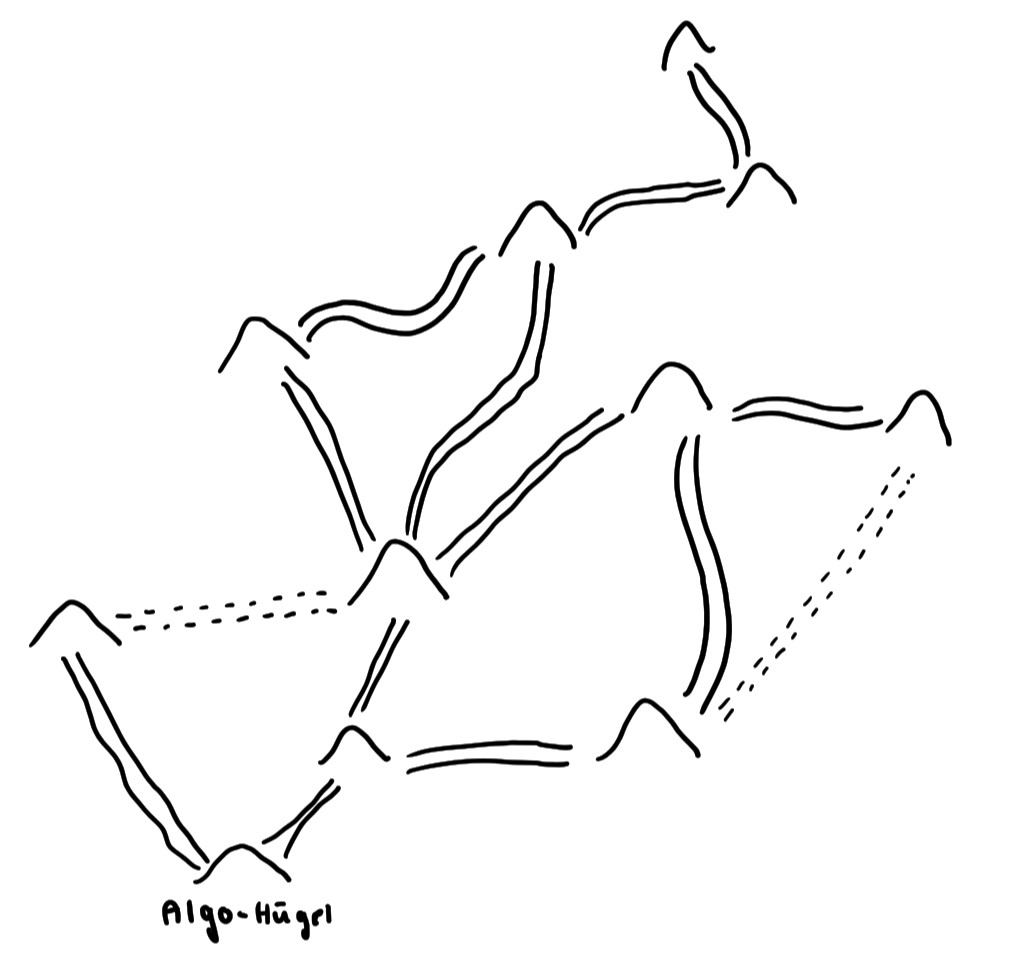Neue WegeMorgens um Punkt 8:00 ging es wieder los und die Ameisen strömten in die verschiedenen Richtungen davon. Iffi hatte sich dem Ameisentrupp angeschlossen, der zu Beginn den linken vom Algo-Hügel ausgehenden Weg verwendete. Als sie die Straße abgelaufen und beim ersten befreundeten Ameisenhügel angekommen waren, warf Iffi einen Blick auf ihre Armbanduhr und sagte: „8:05. Wir haben 5 Minuten für den Weg hierhin gebraucht, wie auch schon bei unserer ersten Messung. Genau wie erwartet.“ Eine andere Ameise nahm ein Schild, trug die Distanz und den vorherigen Ameisenhügel darauf ein und steckte es vor den Ameisenhügel in den Boden.
Ameise mit Armbanduhr„Von diesem Ameisenhügel geht einer der neu entdeckten Wege aus.“, fuhr Iffi fort, „Ich glaube aber nicht, dass wir durch den eine neue kürzeste Route finden, weil der Ameisenhügel, zu dem der Weg hinführt, bei unserer ersten Messung innerhalb von 2 Minuten erreicht wurde.“
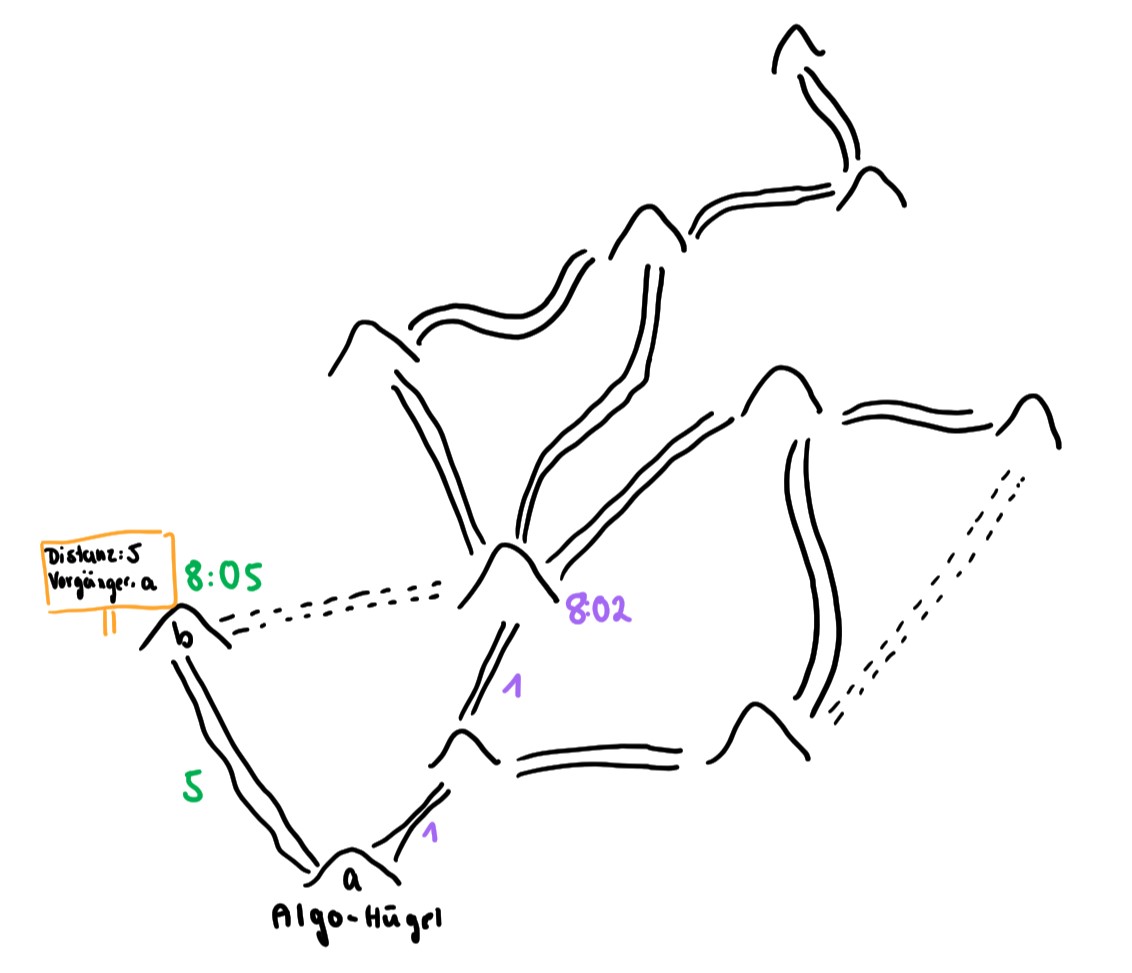Grün: Iffis Ameisentrupp; Lila: Schnellerer Ameisentrupp„Perfekt, dann können wir ja eigentlich nach Hause gehen“, warf Fabian der Faule ein.
„Der Vollständigkeit halber sollten wir den Weg trotzdem vermessen, finde ich“, entgegnete Amelie, die ambitionierte Ameise. Die anderen stimmten ihr zu. Der neue Weg führte durch einen langen, hohlen Baumstamm, der schon langsam verrottete und einen modrigen Gestank von sich gab. Drinnen war es so dunkel, dass man kaum etwas sehen konnte, aber die Ameisen krabbelten unerschrocken immer und immer weiter. Als sie am Ende angelangt waren, traten sie ins gleißende Licht und erblickten den Ameisenbau. Iffi warf wieder einen Blick auf ihre Uhr, doch dieses Mal stutzte sie: „8:01? Das kann doch gar nicht sein, ich glaube meine Uhr ist kaputt.“
„Also meine Uhr zeigt auch 8:01 an“, meinte die Ameise neben ihr. „Meine auch!“, verkündete eine andere, „Bei mir ist es auch 8:01“, sagte die nächste irritiert.
„Dann wird es wohl 8:01 sein“, verkündete Emil die Empirik-Ameise.
„So ein Quatsch, das kann doch gar nicht sein. Wir sind um 8:05 am letzten Ameisenbau aufgebrochen, wie können wir denn früher ankommen, als wir aufgebrochen sind?“, rief Iffi ungläubig.
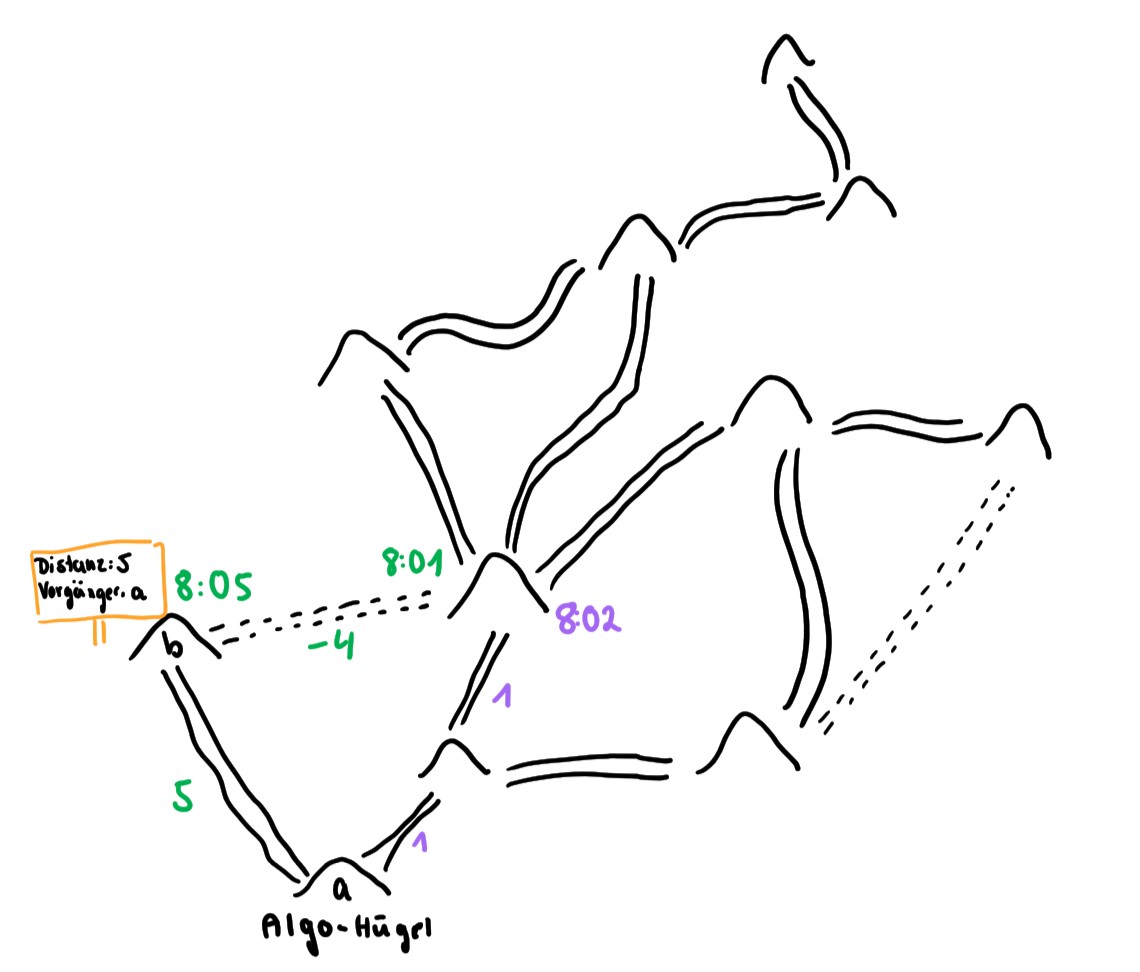Ankunft um 8:01„Ich sehe da nur eine Möglichkeit“, meinte Emil, „Wir haben wohl eine Zeitreise gemacht.“ Iffi starrte sie entgeistert an. Das konnte doch nicht Emils Ernst sein! Andererseits fiel ihr gerade auch keine bessere Erklärung ein.
„Ich denke auch, dass wir eine Zeitreise gemacht haben, in den Chroniken unseres Ameisenbaus ist von einem magischen Baumstamm die Rede, der Eigenschaften hat, die nicht mit unserem heutigen Ameisenweltbild zusammenpassen“, überlegte Sabine die Sagen-Ameise.
Iffi wurde das alles langsam unheimlich. Trotzdem versuchte sie, cool zu bleiben, und sagte lässig: „Na schön. Dann lasst uns mal überlegen, was das für Auswirkungen hat, wenn wir tatsächlich in die Vergangenheit gereist sind und es 8:01 ist. Das heißt dann, dass der andere Ameisentrupp, von dem wir dachten, dass er vor uns hier ankommt, weil er nur 2 Minuten hierhin braucht, noch unterwegs ist. Dann sind wir tatsächlich die ersten, die diesen Hügel erreicht haben und wir haben einen neuen, kürzesten Weg entdeckt.“
Die anderen Ameisen nickten zustimmend. „Wunderbar“, meinte eine Ameise erfreut, „Dann können wir ja gleich ein neues Schild setzen und dem anderen Trupp zuvorkommen.“
Noch nicht ganz überzeugt schien Philip die Physiker-Ameise zu sein. „Ich weiß zwar nicht, was hier gerade passiert ist, aber wenn wir wirklich in die Vergangenheit gereist sind, hat das weit mehr Konsequenzen. Zum Beispiel müsste es uns jetzt alle zweimal geben. Eine Version von unserem Ameisentrupp steht hier, die andere ist gerade erst bei unserem Bau losgekrabbelt und befindet sich auf dem Weg zu dem Ameisenhügel, bei dem wir eben losgelaufen sind. Denn wäre die zweite Version von uns nicht eben losgelaufen, wären wir nie bei diesem Ameisenhügel angekommen...“
„Und was würde passieren, wenn wir jetzt schnell zum vorherigen Ameisenhügel zurückeilen und unsere Klone treffen würden, bevor sie den Baumstamm betreten? Können wir sie dann vom Betreten und von der Durchführung der Zeitreise abhalten und dadurch unsere eigene Anwesenheit hier verhindern? Oder hat unser Handeln ab jetzt keine Auswirkungen auf unsere eigene Vergangenheit und Zukunft, weil wir uns in einer anderen Zeitlinie befinden? In einer, die bis heute um 8:01 identisch ist mit der, aus der wir kommen, aber jetzt durch unser Eintreffen eine andere Wendung nimmt?“
„Das waren alles Probleme, über die Iffi sich lieber keine Gedanken machen wollte. Konnte es nicht doch eine einfachere Erklärung für das Geschehene geben? Sie überlegte fieberhaft...“
„Vielleicht ist es so: Während wir durch den Baumstamm gelaufen sind, sind, aus welchen Gründen auch immer, alle unsere Uhren rückwärts gelaufen. Und jetzt, wo wir wieder hier draußen sind, laufen sie wieder vorwärts.“
Eine besonders mutige Ameise erklärte sich bereit, das Phänomen zu untersuchen und stellte sich für einige Zeit in Sichtweite in den Eingang des Baumstamms. Und tatsächlich: Die Armbanduhr der Ameise schien sich in dieser Zeit erneut rückwärts gedreht zu haben. Iffi seufzte erleichtert und war froh, dass sie nicht, wie Philip beschrieben hatte, in einer fremden Zeit gelandet war.
Da rief eine Ameise: „Hey seht mal, ein anderer Ameisentrupp hat hier schon ein Schild gesetzt. Wir sind nicht die ersten hier!“
Das bestätigte Iffis Theorie natürlich nur weiter. Bis um 8:05 war alles normal verlaufen, dann war ihr Ameisentrupp durch den Baumstamm gelaufen und ihre Uhren hatten sich rückwärts gedreht, während sich die der anderen Ameisentrupps weiterhin vorwärts gedreht hatten. Da Iffis Uhr 8:01 zeigte, und der Abstand zu 8:05 4 Minuten betrug, schloss Iffi, dass sie 4 Minuten lang durch den Baumstamm gelaufen waren. Das hieße, dass es für die anderen Ameisentrupps inzwischen 8:09 wäre.
„Haben wir denn nun einen kürzeren Weg zu diesem Ameisenhügel gefunden oder nicht?“, fragte eine Ameise, „Mit den Uhren der anderen gemessen haben wir 9 Minuten vom Bau bis hierhin gebraucht, aber mit unserer eigenen Uhr nur eine Minute. Von den anderen Ameisentrupps aus betrachtet haben sich unsere Uhren rückwärts gedreht. Aber wer sagt denn, was vor- und rückwärts ist? Vielleicht haben sich unsere Uhren bisher immer rückwärts und jetzt das erste Mal vorwärts gedreht. Dann sollten wir uns nach unserer eigenen Uhr richten.“
Der Fragesteller war Raul die Relativisten-Ameise, die gute Absichten hatte, aber die anderen Ameisen gerade nur umso mehr verwirrte.
„Ich finde auch, dass wir uns ab jetzt nach unserer eigenen Uhr richten sollten“, meinte eine andere Ameise, „Unsere Ameisenkönigin möchte, dass wir möglichst kurze Handelsrouten finden. Wenn wir davon ausgehen, dass es 8:01 ist, haben wir einen neuen kürzesten Weg hierhin gefunden. Das ist im Interesse unserer Königin und wir können ihr diese gute Nachricht überbringen.“
Die anderen Ameisen stimmten zu, was die Königin wollte, das galt.
„Wir sollten das bestehende Schild einfach ersetzen.“, schlug daraufhin jemand vor, nahm das alte Schild und platzierte stattdessen ein Schild mit den neuen Werten. Da hatte Iffi eine Erkenntnis und meinte entsetzt: „Dann müssten wir ja jetzt den anderen Ameisentrupps hinterherlaufen, die von diesem Ameisenhügel aufgebrochen sind. Sie sind der Meinung, um 8:02 hier aufgebrochen zu sein, und die Zeiten, die sie auf allen weiteren Schildern eintragen, hängen von dieser Uhrzeit ab. Diese müssten wir dann auch noch alle ersetzen!“
„Dann machen wir das doch“, meinte eine andere, „Wo ist das Problem?“
„Das dürfen wir nicht. Ich habe der Ameisenkönigin versprochen, dass wir keinen Ameisenhügel doppelt ablaufen, ansonsten hätte sie mir dieses Vorhaben nie genehmigt!“, erklärte Iffi verzweifelt.
In der Menge brachen laute Diskussionen aus, gab es doch keine Möglichkeit, es der Ameisenkönigin an dieser Stelle recht zu machen. Erschöpft ließ Iffi sich auf den Boden sinken. Ihre Idee hatte beim letzten Mal so reibungslos funktioniert, aber heute überhaupt nicht. Aber das Auftreten einer Zeitanomalie hatte sie wirklich nicht vorausahnen können. Also blieb ihr keine andere Möglichkeit, als das Unterfangen abzubrechen und ihr Versagen vor der Ameisenkönigin zuzugeben.
Währenddessen bei den Weinbergschnecken
„Arme Iffi“, sagte Timmi, „Das sowas passieren kann, hätte wohl keiner gedacht.“
„Genau“, pflichtete Wanda Timmi bei, „Aber das Problem, auf das Iffi gestoßen ist, ist auch ein allgemeines Problem bei der Anwendung des Dijkstra-Algorithmus. Bei negativen Kantengewichten erzeugt der Algorithmus kein korrektes Ergebnis und findet nicht die kürzesten Wege.“
„Stimmt“, meinte Timmi, „Übertragen wir das Netz von Ameisenhügeln auf einen Graphen, haben wir an der Kante, die den Baumstamm darstellt, ein Kantengewicht von -4. Das führt aus dem selben Grund wie bei unseren Ameisen zu Problemen: Durch das negative Kantengewicht wird ein kürzerer Weg gefunden und die Distanz des so erreichten Knotens auf 1 gesetzt, allerdings wurde die vorherige Distanz, nämlich 2, schon an alle weiteren Nachbarknoten von diesem propagiert. In allen folgenden Knoten entstehen so falsche Werte für die Distanz und den Vorgängerknoten. So, wie unser Algorithmus formuliert ist, werden diese aber nicht korrigiert, da jeder Knoten nur einmal betrachtet wird.“
„Sind keine negativen Kantengewichte vorhanden, tritt das Problem nicht auf“, ergänzte Wanda, „So kann es zwar passieren, dass ein kürzerer Weg zu einem Knoten gefunden wurde und die Distanz und der Vorgängerknoten angepasst werden müssen, jedoch wurden diese Werte dann noch nicht an die Nachbarknoten weitergegeben, da diese noch nicht entdeckt wurden.“
Eine helfende Hand
Iffi hatte seit Tagen kein Auge zugetan. Die Ameisenkönigin war alles andere als erfreut gewesen, als Iffi ohne eine neue Karte zu ihr zurückgekehrt war. Außerdem hatten die anderen Ameisenkolonien Wind von Iffis Idee bekommen und hatten nun auch begonnen, die kürzesten Transportrouten für ihren jeweiligen Ameisenhügel zu berechnen. Dadurch hatte sich vor den Ameisenhügeln ein regelrechter Schilderwald entwickelt und keiner machte Anstalten, die jeweiligen Schilder wieder wegzuräumen. Iffis Expedition markierte daher den Anfang von einer Verschlechterung der interhügeligen Beziehungen zu den anderen Ameisenkolonien, was den Bewohnern des Algo-Hügels auf kurz oder lang wirklich schaden konnte. Auf weitere Genehmigungen für zukünftige Unternehmungen konnte Iffi sich also erstmal nicht einstellen und ihre Karriere beim Ameisenministerium konnte sie auch vergessen. Aber so leicht gab sie nicht auf. Sie hatte die Listen mit den Dauern, die die Ameisen für die einzelnen Straßen benötigt hatten, mitgenommen. Vielleicht konnte sie ja die kürzesten Wege mithilfe der Listen ganz allein berechnen.
Eine Möglichkeit bestand daraus, die Dauer für alle möglichen Routen von einem zum anderen Hügel auszurechnen und die mit der kürzesten zur kürzesten Route zu erklären. Aber dazu hatte Iffi keine Lust, das würde selbst schon bei den wenigen Ameisenhügeln auf der Wiese lange dauern. Und das Konzept, das sie bisher angewendet hatte, schien ja nicht zu funktionieren, ohne dass sie alle Ameisenhügel mehrmals betrachtete, was unter Umständen auch wieder lange dauern könnte. Sie brauchte ein neues Konzept. Es musste doch eine Möglichkeit geben, die kürzesten Wege aus den ihr vorliegenden Daten zu rekonstruieren. Im Übrigen fragte sie sich sowieso, warum sie nicht von vornherein einfach die zugehörigen Dauern zu den Straßen gemessen und das Problem dann von Hand an ihrem Schreibtisch gelöst hatte. Ihre Schneckenfreunde Wanda und Timmi hätten ihr sicher geholfen. Ha! Die beiden konnte sie jetzt um Rat fragen!
„Hmmmm“, sagte Wanda nachdenklich und zerraspelte dabei gemächlich ein Salatblatt. „Ich denke, das kriegen wir hin“, behauptete sie und schluckte ein Stück.
„Und wie?“, fragte Iffi aufgeregt.
„Nun ja“, sagte Timmi und neigte die Stielaugen zu Iffi hinunter, „Du könntest den Floyd-Warshall-Algorithmus verwenden. Dieser erzeugt auch bei negativen Kantengewichten ein korrektes Ergebnis. Allerdings liegt seine Laufzeit in Θ(n³), also wenn du es besonders eilig hast, ist dieser vielleicht nicht die beste Wahl.“
Iffi hatte nicht viel davon verstanden, aber Timmi schien ihr gerade eine Lösung auf dem Silbertablett zu servieren, so viel war ihr klar.
„Und wie funktioniert der Algorithmus?“, fragte sie interessiert.
„Nun ja“, sagte Wanda, „Der Algorithmus basiert auf einer rekursiven Formel. Dazu betrachten wir den Weg von einem Knoten i zu einem Knoten j über einen Zwischenknoten k. Ist der uns bisher bekannte Weg von i nach j länger als der Weg von i nach j, wenn wir über den Zwischenknoten k gehen, haben wir einen neuen kürzesten Weg von i nach j gefunden, nämlich den über k.“
Iffi schaute Wanda fragend an. „Wir können das als Rekursion δ notieren, die uns die Länge des kürzesten Weges berechnet“, meinte Wanda, und sagte:
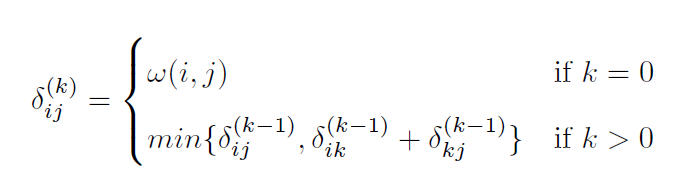
„Toll. Und was soll ich jetzt damit anfangen?“, fragte Iffi genervt.
„Du nummerierst erstmal alle deine Knoten von 0 bis n durch. Die Nummern kannst du für die Indizes i, j und k verwenden und so die Formel auf die Knoten anwenden. Interessierst du dich für den kürzesten Weg von i nach j, musst du δ(n)ij berechnen.“
Iffi überlegte kurz, und meinte dann: „Ok, hab’s verstanden. Das mache ich dann für alle Wege von unserem Ameisenhügel zu den anderen Hügeln. Dann kann ich ja loslegen. Vielen Dank!“
„Nicht so hastig“, meinte Timmi und schielte auf ein köstlich aussehendes Stück Gurke neben Iffi, „Wenn du das so machst, kommst du zwar auf ein richtiges Ergebnis, aber du wirst seeehr lange brauchen. Vielleicht ahnst du ja auch schon, warum.“
„Nein“, seufzte Iffi, „Erklär’s mir.“
„Rekursive Algorithmen haben oft eine hohe Laufzeit. Das liegt daran, dass es oft mehr als einen rekursiven Aufruf benötigt, um ein Ergebnis zu berechnen. Bei dieser Rekursion muss δ gleich 3 Mal rekursiv aufgerufen werden, um ein Ergebnis zu bestimmen. Für jeden dieser 3 Aufrufe auch wieder 3 Aufrufe benötigt werden und so weiter, bis k = 0 gilt. Dazu muss k n-mal dekrementiert werden. Dadurch läge die Laufzeit des Algorithmus in Θ(3ⁿ) und wäre exponentiell.“
„Also sollte ich die Rekursion nicht so ohne Weiteres verwenden“, schloss Iffi, „Aber wie soll ich den Algorithmus denn stattdessen umsetzen?“
„Du kannst dir überlegen, dass viele Werte mehrfach berechnet werden. Beispielsweise könnte es sein, dass δ(k-1)ij und δ(k-1)ik einen gemeinsamen Teilweg enthalten, den wir in den beiden rekursiven Aufrufen dann doppelt berechnen.“
„Aber ich führe die Rechnungen für die beiden Aufrufe ja nacheinander aus, dann kann ich mir den gemeinsamen Teilweg ja auch einfach notieren und spare mir das doppelte Berechnen“, schlug Iffi vor.
„Das ist der richtige Ansatz“, lobte Wanda sie, „Wir müssen all unsere Ergebnisse für δ(k)ij zwischenspeichern. So können wir sichergehen, dass kein Ergebnis für einen Aufruf doppelt berechnet wird und unsere Laufzeit so gering ist, wie bei diesem Algorithmus möglich ist. Da wir bei δ(k)ij 3 Variablen haben, bietet es sich an, diese in k n × n-Matrizen zu speichern, wobei i der Zeilen- und j der Spaltenindex wäre. Das Prinzip nennt sich dynamische Programmierung.“
Timmi erklärte weiter: „Unser Algorithmus benutzt nun also die Ergebnisse aus der (k-1)-ten Matrix, um Werte in der k-ten Matrix zu bestimmen. Daher bietet es sich an, den Algorithmus iterativ statt rekursiv aufzubauen und die Matrizen beginnend bei k=0 bis n zu füllen. Hier, das ist der Pseudocode.“
Da fiel Iffi etwas auf: „Wenn wir eine n × n-Matrix verwenden und i unser Start- und j unser Endknoten ist, dann haben wir ja nach dem Durchlauf unseres Algorithmus den kürzesten Weg von jedem Ameisenhügel zu allen anderen Ameisenhügeln bestimmt. Das ist ja super, dann kann ich das Ergebnis mit den anderen Ameisenkolonien teilen und sie müssen die kürzesten Wege gar nicht selbst nochmal berechnen!“
Iffi freute sich. Wanda und Timmi hatten ihr nicht nur gezeigt, wie sie ihre letztens gescheiterte Arbeit doch noch fortsetzen konnte, sondern hatten ihr auch eine Möglichkeit gegeben, die Beziehungen zu den anderen Ameisenhügeln wieder zu verbessern. Und tatsächlich: Mithilfe des Floyd-Warshall-Algorithmus konnte sie alle kürzesten Wege berechnen, ohne dass der magische Baumstamm und seine zugehörige Reisedauer von -4 Minuten ein Problem darstellte. Die anderen Ameisenhügeloberhäupter hatten das Chaos der letzten Tage schnell vergessen, als Iffi ihnen eine gemeinsame Karte mit allen kürzesten Wegen präsentierte und beschlossen, bei Problemen dieser Art in Zukunft enger zusammenzuarbeiten. Auch die Ameisenkönigin Amanda war hocherfreut und beförderte Iffi zur Ameisenministerin für Algorithmen.
Kommentare
Noch Fragen?