Komplexer Zahlenrechner in Rust

Um in Rust loszulegen, habe ich einen Zahlenrechner implementiert. Er kann Berechnungen mit reellen Zahlen sowie mit komplexen Zahlen durchführen. Außerdem bietet er einige Funktionen zum Berechnen von Summen oder Produkten. Ich habe dann egui verwendet, um eine GUI dafür zu erstellen.

GUI

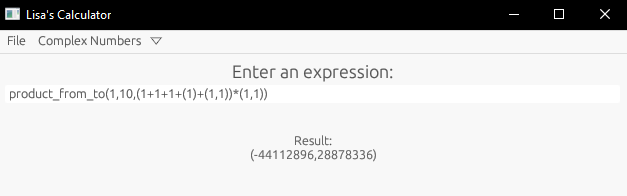
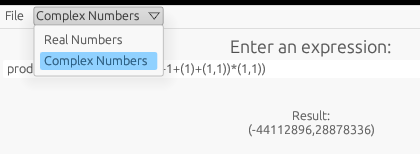
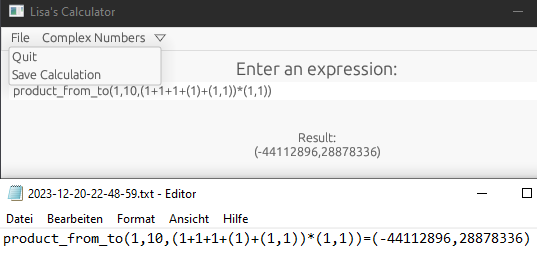
Benutzer können den arithmetischen Ausdruck und das Ergebnis in eine Datei speichern.

Generische Traits für Körper

Der Quellcode meines Rechners kann leicht erweitert werden, um mit jedem Körper zu arbeiten, nicht nur mit reellen oder komplexen Zahlen. Daher habe ich den Code für die eigentlichen Berechnungen in ein Rust Trait solid verschoben.

pub trait Solid<T : SolidNumber<T>> : Sized {
        //general info
        fn get_solid_name() -> String;

        //addition
        fn get_neutral_element_addition() -> T;
        fn add(x : T, y : T) -> T;
        fn get_additive_inverse(x : T) -> T;

        //multiplication
        fn get_neutral_element_multiplicative() -> T;
        fn multiply(x : T, y : T) -> T;
        fn get_multiplicative_inverse(x : T) -> T;

        //other functions
        fn get_available_functions() -> Vec<(String, fn(Vec<String>)->(T, String), Vec<i32>, i32)>;
}

Dieser generische Trait wird verwendet, um reale und komplexe Zahlen zu implementieren:

use std::fmt::Display;
use chrono::format::parse;
use crate::calculations::calculator::calculatorfunctions::{Calculator, has_enclosing_brackets, split_to_expressions};
use crate::calculations::calculator::solid::solid::{get_standard_methods, PrintableNumber, Solid, SolidNumber};
use crate::calculations::solids::realnumbers::RealNumbers;

pub struct ComplexNumbers{

}

pub struct ComplexNumber {
    a : f64,
    b : f64,
}



impl Solid<ComplexNumber> for ComplexNumbers{
    fn get_solid_name() -> String {
        return "Complex Numbers".to_string();
    }

    fn get_neutral_element_addition() -> ComplexNumber {
        return ComplexNumber { a: 0.0, b: 0.0 };
    }

    fn add(x: ComplexNumber, y: ComplexNumber) -> ComplexNumber {
        return ComplexNumber {a : x.a+y.a, b: x.b+y.b};
    }

    fn get_additive_inverse(x: ComplexNumber) -> ComplexNumber {
        return ComplexNumber {a : -x.a, b: -x.b};
    }

    fn get_neutral_element_multiplicative() -> ComplexNumber {
        return ComplexNumber{ a: 1.0, b: 0.0 }
    }

    fn multiply(x: ComplexNumber, y: ComplexNumber) -> ComplexNumber {

        let a = x.a;
        let b = x.b;
        let c = y.a;
        let d = y.b;
        return ComplexNumber{
            a : a * c - b * d,
            b: a * d + c * b
        };
    }

    fn get_multiplicative_inverse(x: ComplexNumber) -> ComplexNumber {
        let nenner = (x.a.powi(2) + x.b.powi(2));
        return ComplexNumber{a: x.a/ nenner,b: -(x.b/nenner)};
    }

    fn get_available_functions() -> Vec<(String, fn(Vec<String>) -> (ComplexNumber, String), Vec<i32>, i32)> {
        return get_standard_methods::<ComplexNumber, ComplexNumbers>();
    }
}


impl PrintableNumber for ComplexNumber {
    fn to_sn_string(&self) -> String {
        return format!("({},{})",self.a,self.b)
    }
}

impl SolidNumber<ComplexNumber> for ComplexNumber {
    fn is_number(s: &str) -> bool {
        if !has_enclosing_brackets(&s.to_string()) {
            if Calculator::<f64, RealNumbers>::parse(s).1==""{
                return true;
            }
            if s.eq("i"){
                return true;
            }

            return false;
        }
        else{
            let numbers = split_to_expressions(&s.to_string(), vec![',']);

            if  numbers.0.len()!=2{
                return false;
            }
            //println!("complex number: a={}, b={}", numbers.0[0], numbers.0[1]);
            let a = Calculator::<f64, RealNumbers>::parse(numbers.0[0].as_str());
            let b = Calculator::<f64, RealNumbers>::parse(numbers.0[1].as_str());

            if (a.1!="") | (b.1!=""){
                return false;
            }

            return true;
        }
    }

    fn from_string(s: String) -> ComplexNumber {
        if s.eq("i"){
            return ComplexNumber{a: 0.0, b: 1.0};
        }
        let parsedFloat = Calculator::<f64, RealNumbers>::parse(s.as_str());
        if parsedFloat.1==""{
            return ComplexNumber{a : parsedFloat.0, b: 0.0};
        }

        let numbers = split_to_expressions(&s.to_string(), vec![',']);
        let a = Calculator::<f64, RealNumbers>::parse(numbers.0[0].as_str());
        let b = Calculator::<f64, RealNumbers>::parse(numbers.0[1].as_str());
        return ComplexNumber {a: a.0, b: b.0 };

    }


}

Das Projekt ist auch hier zu finden:

GitHub

Kommentare

Noch Fragen?

Durch das Anmelden mit Github wird ein Login-Cookie erstellt und gespeichert. Sie können dies jederzeit rückgängig machen, indem Sie 'Cookie löschen' anklicken.